RIGHT STUFF, Inc.

Right Stuff Wrong Stuff

ガレージを作る（天井部分の強度検討）

ここをガレージにするにあたっての一番の問題点。それは二階のゴミでした。ここは灰屋だったので昔は堆肥を作っており、その原料となる藁などは二階に置いてあったのです。子供の頃はその藁の中に入って遊んだ記憶があります。

今は藁は置いてありませんが、その名残で廃材を利用した床板や藁などのかすが沢山残っています。これが少しずつ上から降ってきて部品にたまり、それが湿気を呼んで下手をすると屋外よりも早く錆びてしまいます。

これ以上バイクや工具を痛めないためには早急に天井が必要です。さらに、この部分は梯子を掛ければ登れる構造になっていますし、今までは簡易的な2階として使っていた歴史が有ります。私を含めて誰かがうっかりして登るかもしれません。そのために単純な天井では無くて昔どおりに簡易的な2階の床として検討する事も必要です。

稲家の建物はある程度の広さがあります。「2階を作る」などと言えば堅苦しいお役所から「建築士の資格が・・・」等と言われそうな気もします。でも今回の行為はあくまでも「百姓のオヤジが、痛んだ灰屋の床をホームセンターで買ってきた板で修理する」行為なので問題は無いでしょう。筑豊的に処理するなら「がたがた言うなっちゃ。しゃあしいっちゃ！」の世界です（笑）。

とりあえず加重を想定します。製鉄所の点検デッキなどでは200kg/m²程度の加重を指定される事が多いように記憶しています。建築基準法を調べてみると住居では180kg/m²と言う数値が出てきました。根太などと合わせて200kg/m²と考えれば同じ様な感じです。そこで今回も200kg/m²→2000N/m²を想定される加重条件とすることにしました。

床板と根太は、一般的な材料を一般的な配置で使用する限り大きな問題は無いと考えて検討しません。大中小の梁の曲げに関してだけ検討することにしました。

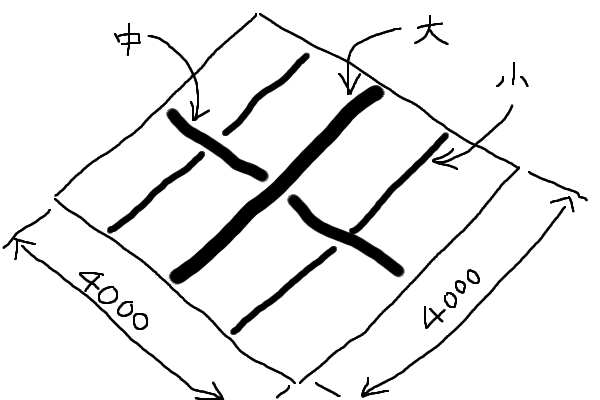
ここには梁配置の説明図があります。

梁の配置は上図の様になっており、最小の区画は2mx1mの区画になります。同じ配置がずーと続いている訳では無いので、1mあたり何Nと考えると不味いかもしれません。建築屋さんはどうやるのか良くわからなかったので、悪い方に考えて1mx1mの所に仮想の梁を想定し、その梁の両端支持加重を両側の梁に集中加重として加える事にしました。

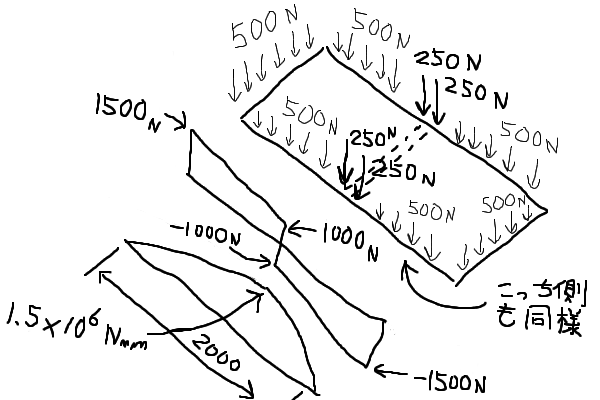
小梁の計算

ここには小梁の図が有ります。

集中加重によるモーメントは　1000x1000=1.00x10⁶Nmm
等分布加重によるモーメントは　(1/8)x(1000/1000)x2000²=5.00x10⁵Nmm
合計して
M=1.50x10⁶Nmm　が小梁の最大曲げモーメントとなります。

（根太掛けは片面からしか加重を受けませんから、これの半分が根太掛けの応力条件となるはずです。）

最大モーメント部の断面は90mmx90mmを使う予定なので、この部分の断面係数は
Z=(1/6)x90³=1.22x10⁵mm³となります。

これより小梁の最大応力は
σ=M/Z=(1.50x10⁶)/(1.22x10⁵)=12.3N/mm²です。

ここで材料として最低の杉材を用いるとすれば基準の曲げ応力は18N/mm²となります。これより長期の許容応力は6.60N/mm²。短期の許容応力は12.0N/mm²が算出されます。

以上より木材の質が悪ければ、短期の許容応力に対してもぎりぎりであることが解ります。しかしここでの前提は非常に厳しいので楽な場合も検討してみます。

もし延々と続く梁と考えれば加重条件は1mあたり2000Nが加わる事になります。これなら曲げモーメントは
M=(1/8)x(2000/1000)x2000²=1.00x10⁶Nmmとなります。
この時の最大応力は
σ=M/Z=(1.00x10⁶)/(1.22x10⁵)=8.20N/mm²です。

これなら最低の材を使っても短期的には十分な強度となりますし、木材の質が高くて基準の曲げ応力を27N/mm²程度と考えれば許容応力が、長期9.90N/mm²、短期18.0N/mm²まで向上しますから、長期的にも大丈夫な範囲となります。

また、現時点でこの部分にはΦ65程度の丸太が使ってあり上面に根太を打ち付けるのが困難です。仕口の取り合いや他の梁とのバランスから90角程度が工作的に楽です。

以上より総合的に？？判断して、「今回の目的なら90角で良いんじゃないの」とします。たわみに関しては自分がふわふわ感を我慢すればよいので無視します（笑）。

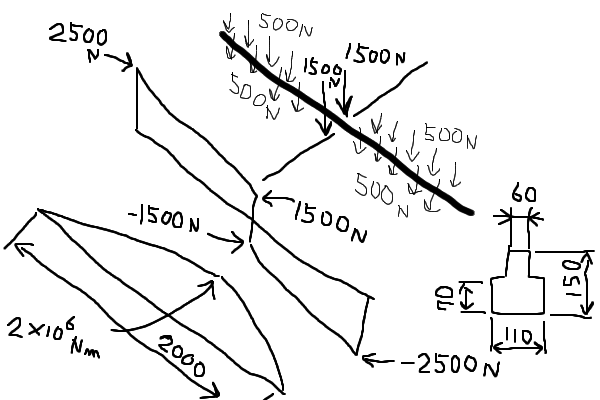
中梁の計算

ここには中梁の図が有ります。

集中加重によるモーメントは　1500x1000=1.50x10⁶Nmm
等分布加重によるモーメントは　(1/8)x(1000/1000)x2000²=5.00x10⁵Nmm
合計して
M=2.00x10⁶Nmm　が中梁の最大曲げモーメントとなります。

小梁と違って中梁の最弱断面は単純ではありません。小梁を掛けるために仕口の切り欠きがあるからです。昔作った表計算を使って、この部分の図心は下から63.8mmで断面係数は上がZ=2.59x10⁵mm³。下が3.50x10⁵mm³となりました。

小さい方の断面係数でチェックすれば、中梁の最大応力は
σ=M/Z=(2.00x10⁶)/(2.59x10⁵)=7.70N/mm²となります。

中梁の材質は堅めの木材で断面はほぼ四角形に整形してあります。強度が十分であればこのまま使いたい所です。小梁と同様な基準で判断して、「今回の目的なら現状の中梁を継続使用して良い」とします。

実際は引っ張り側の断面係数は上記計算の1.3倍程度有ります。また、弱い方の圧縮側には小梁のほぞがかみ合っていますので、ある程度まで圧縮されればこれが効いてくるでしょう。破壊までを考えると小梁よりもかなり安心して良いと思われます。

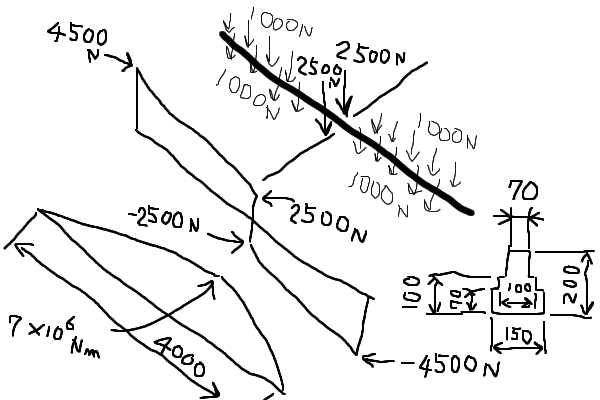
大梁の計算

ここには大梁の図が有ります。

集中加重によるモーメントは　2500x2000=5.00x10⁶Nmm
等分布加重によるモーメントは　(1/8)x(1000/1000)x4000²=2.00x10⁶Nmm
合計して
M=7.00x10⁶Nmm　が大梁の最大曲げモーメントとなります。

大梁の最弱断面も単純ではありません。こちらも昔作った表計算を使って計算します。最弱断面の図心は下から81.6mmで断面係数は上がZ=8.20x10⁵mm³。下が8.08x10⁵mm³となりました。

小さい方の断面係数でチェックすれば、大梁の最大応力は
σ=M/Z=(7.00x10⁶)/(8.08x10⁵)=8.66N/mm²となります。

大梁の材質も堅めの木材で断面はほぼ四角形に整形してあります。こちらも強度が十分であればこのまま使いたい所です。同様な基準で判断してこの大梁も、「今回の目的なら現状の大梁を継続使用して良い」とします。

大梁に関してはスパンが4mも有るのでたわみの影響が出てくるかもしれません。ただ、この上に根太を打ち付けてその上には15mmの床板が付きます。結合度は低いとは思いますが、ある程度組み合わせ梁として働くと期待して、あまりボヨンボヨンしないと思いこむことにします。

梁の太さを計算してみると大変面白い結果が出ました。大昔の田舎の大工さんがこういう計算をしていたとは思えません。たぶん長年の経験から太さを決めているのだと思います。それでも各部の応力をほとんど同じレベルにまとめ上げてありました。驚きました。

隣接した稲家の2階はこれよりも相当しっかりとした作りです。半間ごとに高さが250mmくらいある大引が並んでいていかにも丈夫そうです。灰屋は壁もありませんから簡易的な床と考えていたのでしょう。両者にきちんと強度の差を付けて作ってある所も面白いです。